Antiderivative of sine x. Methods for integrating trigonometric functions. Integrals of the product of a polynomial and sine or cosine

Basic trigonometric formulas and basic substitutions are presented. Integration methods are outlined trigonometric functions- integration of rational functions, product power functions from sin x and cos x, product of a polynomial, exponential and sine or cosine, integration of inverse trigonometric functions. Non-standard methods are affected.

Content

Standard methods for integrating trigonometric functions

General approach

First, if necessary, the integrand must be transformed so that the trigonometric functions depend on a single argument, which is the same as the integration variable.

For example, if the integrand depends on sin(x+a) And cos(x+b), then you should perform the conversion:
cos (x+b) = cos (x+a - (a-b)) = cos (x+a) cos (b-a) + sin ( x+a ) sin (b-a).
Then make the replacement z = x+a. As a result, trigonometric functions will depend only on the integration variable z.

When trigonometric functions depend on one argument that coincides with the integration variable (let's say it's z), that is, the integrand consists only of functions like sin z, cos z, tg z, ctg z, then you need to make a substitution
.
Such a substitution leads to the integration of rational or irrational functions (if there are roots) and allows one to calculate the integral if it is integrated in elementary functions.

However, you can often find other methods that allow you to evaluate the integral in a shorter way, based on the specifics of the integrand. Below is a summary of the main such methods.

Methods for integrating rational functions of sin x and cos x

Rational functions from sin x And cos x are functions formed from sin x, cos x and any constants using the operations of addition, subtraction, multiplication, division and raising to an integer power. They are designated as follows: R (sin x, cos x). This may also include tangents and cotangents, since they are formed by dividing sine by cosine and vice versa.
Integrals of rational functions have the form:
.

Methods for integrating rational trigonometric functions are as follows.
1) Substitution always leads to the integral of a rational fraction. However, in some cases, there are substitutions (these are presented below) that lead to shorter calculations.
2) If R (sin x, cos x) cos x → - cos x sin x.
3) If R (sin x, cos x) multiplied by -1 when replacing sin x → - sin x, then the substitution t = cos x.
4) If R (sin x, cos x) does not change as with simultaneous replacement cos x → - cos x, And sin x → - sin x, then the substitution t = tg x or t = ctg x.

Examples:
, , .

Product of power functions of cos x and sin x

Integrals of the form

are integrals of rational trigonometric functions. Therefore, the methods outlined in the previous section can be applied to them. Methods based on the specifics of such integrals are discussed below.

If m and n are rational numbers, then one of the substitutions t = sin x or t = cos x the integral is reduced to the integral of the differential binomial.

If m and n are integers, then integration is performed using reduction formulas:

;
;
;
.

Example:
.

Integrals of the product of a polynomial and sine or cosine

Integrals of the form:
, ,
where P(x) is a polynomial in x, are integrated by parts. This gives the following formulas:

;
.

Examples:
, .

Integrals of the product of a polynomial, exponential and sine or cosine

Integrals of the form:
, ,
where P(x) is a polynomial in x, integrated using Euler’s formula
e iax = cos ax + isin ax(where i 2 = - 1 ).
To do this, using the method outlined in the previous paragraph, calculate the integral
.
By separating the real and imaginary parts from the result, the original integrals are obtained.

Example:
.

Non-standard methods for integrating trigonometric functions

Below are a number of non-standard methods that allow you to perform or simplify the integration of trigonometric functions.

Dependence on (a sin x + b cos x)

If the integrand depends only on a sin x + b cos x, then it is useful to apply the formula:
,
Where .

For example

Resolving fractions from sines and cosines into simpler fractions

Consider the integral
.
The simplest method of integration is to decompose the fraction into simpler ones using the transformation:
sin(a - b) = sin(x + a - (x + b)) = sin(x+a) cos(x+b) - cos(x+a) sin(x+b)

Integrating fractions of the first degree

When calculating the integral
,
it is convenient to isolate the integer part of the fraction and the derivative of the denominator
a 1 sin x + b 1 cos x = A (a sin x + b cos x) + B (a sin x + b cos x)′ .
The constants A and B are found by comparing the left and right sides.

References:
N.M. Gunther, R.O. Kuzmin, Collection of problems on higher mathematics, "Lan", 2003.

Integration of functions rationally dependent on trigonometric functions

1. Integrals of the form ∫ sin n xdx , ∫ cos n xdx , n>0
a) If n is odd, then one power of sinx (or cosx) should be entered under the sign of the differential, and from the remaining even power should be passed to the opposite function.
b) If n is even, then we use formulas for reducing the degree
2. Integrals of the form ∫ tg n xdx , ∫ ctg n xdx , where n is an integer.
Formulas must be used

3. Integrals of the form ∫ sin n x cos m x dx
a) Let m and n be of different parities. We use the substitution t=sin x if n is odd or t=cos x if m is odd.
b) If m and n are even, then we use formulas for reducing the degree
2sin 2 x=1-cos2x , 2cos 2 x=1+cos2x .
4. Integrals of the form

If the numbers m and n are of the same parity, then we use the substitution t=tg x. It is often convenient to use the trigonometric unit technique.
5. ∫ sin(nx) cos(mx)dx , ∫ cos(mx) cos(nx)dx , ∫ sin(mx) sin(nx)dx

Let's use the formulas for converting the product of trigonometric functions into their sum:

sin α cos β = ½(sin(α+β)+sin(α-β))
cos α cos β = ½(cos(α+β)+cos(α-β))
sin α sin β = ½(cos(α-β)-cos(α+β))

Examples
1. Calculate the integral ∫ cos 4 x·sin 3 xdx .
We make the replacement cos(x)=t. Then ∫ cos 4 x sin 3 xdx =
2. Calculate the integral.
Making the replacement sin x=t , we get

3. Find the integral.
We make the replacement tg(x)=t . Substituting, we get

Integrating expressions of the form R(sinx, cosx)

Example No. 1. Calculate integrals:

Solution.
a) Integration of expressions of the form R(sinx, cosx), where R is a rational function of sin x and cos x, are converted into integrals of rational functions using the universal trigonometric substitution tg(x/2) = t.
Then we have

A universal trigonometric substitution makes it possible to go from an integral of the form ∫ R(sinx, cosx) dx to an integral of a fractional rational function, but often such a substitution leads to cumbersome expressions. Under certain conditions, simpler substitutions are effective:

If the equality R(-sin x, cos x) = -R(sin x, cos x)dx is satisfied, then the substitution cos x = t is applied.
If the equality R(sin x, -cos x) = -R(sin x, cos x)dx holds, then the substitution sin x = t.
If the equality R(-sin x, -cos x) = R(sin x, cos x)dx holds, then the substitution tgx = t or ctg x = t.

In this case, to find the integral

let us apply the universal trigonometric substitution tg(x/2) = t.
Then Answer:

There will also be problems for you to solve on your own, to which you can see the answers.

The integrand can be converted from the product of trigonometric functions to the sum

Let us consider integrals in which the integrand is the product of sines and cosines of the first degree of x multiplied by different factors, that is, integrals of the form

Using well-known trigonometric formulas

(2)
(3)
(4)
one can transform each of the products in integrals of the form (31) into an algebraic sum and integrate according to the formulas

(5)

(6)

Example 1. Find

Solution. According to formula (2) at

Example 2. Find integral of a trigonometric function

Solution. According to formula (3) at

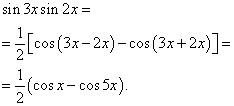
Example 3. Find integral of a trigonometric function

Solution. According to formula (4) at we obtain the following transformation of the integrand:

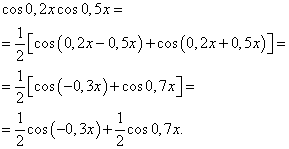
Applying formula (6), we obtain

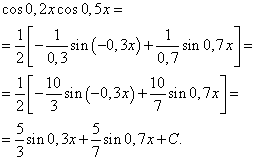
Integral of the product of powers of sine and cosine of the same argument

Let us now consider integrals of functions that are the product of powers of sine and cosine of the same argument, i.e.

(7)

In special cases, one of the indicators ( m or n) may be zero.

When integrating such functions, it is used that an even power of cosine can be expressed through sine, and the differential of sine is equal to cos x dx(or even power of sine can be expressed in terms of cosine, and the differential of cosine is equal to - sin x dx ) .

Two cases should be distinguished: 1) at least one of the indicators m And n odd; 2) both indicators are even.

Let the first case take place, namely the indicator n = 2k+ 1 - odd. Then, given that

The integrand is presented in such a way that one part of it is a function of only the sine, and the other is the differential of the sine. Now using variable replacement t= sin x the solution reduces to integrating the polynomial with respect to t. If only the degree m is odd, then they do the same, isolating the factor sin x, expressing the rest of the integrand in terms of cos x and believing t=cos x. This technique can also be used when integrating the quotient powers of sine and cosine , When at least one of the indicators is odd . The whole point is that the quotient of the powers of sine and cosine is a special case of their product : When a trigonometric function is in the denominator of an integrand, its degree is negative. But there are also cases of partial trigonometric functions, when their powers are only even. About them - in the next paragraph.

If both indicators m And n– even, then, using trigonometric formulas

reduce the exponents of sine and cosine, after which an integral of the same type as above is obtained. Therefore, integration should be continued according to the same scheme. If one of the even exponents is negative, that is, the quotient of even powers of sine and cosine is considered, then this scheme is not suitable . Then a change of variable is used depending on how the integrand can be transformed. Such a case will be considered in the next paragraph.

Example 4. Find integral of a trigonometric function

Solution. The cosine exponent is odd. Therefore, let's imagine

t= sin x(Then dt=cos x dx ). Then we get

Returning to the old variable, we finally find

Example 5. Find integral of a trigonometric function

Solution. The cosine exponent, as in the previous example, is odd, but larger. Let's imagine

and make a change of variable t= sin x(Then dt=cos x dx ). Then we get

Let's open the brackets

and we get

Returning to the old variable, we get the solution

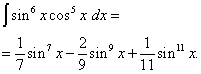
Example 6. Find integral of a trigonometric function

Solution. The exponents of sine and cosine are even. Therefore, we transform the integrand function as follows:

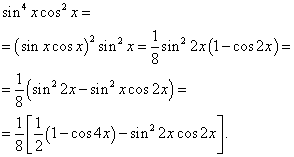
Then we get

In the second integral we make a change of variable, setting t= sin2 x. Then (1/2)dt= cos2 x dx . Hence,

Finally we get

Using the Variable Replacement Method

Variable Replacement Method when integrating trigonometric functions, it can be used in cases where the integrand contains only sine or only cosine, the product of sine and cosine, in which either sine or cosine is in the first degree, tangent or cotangent, as well as the quotient of even powers of sine and cosine of one and the same argument. In this case, it is possible to perform permutations not only sin x = t and sin x = t, but also tg x = t and ctg x = t .

Example 8. Find integral of a trigonometric function

Solution. Let's change the variable: , then . The resulting integrand can be easily integrated using the table of integrals:

Example 9. Find integral of a trigonometric function

Solution. Let's transform the tangent into the ratio of sine and cosine:

Let's change the variable: , then . The resulting integrand is table integral with a minus sign:

Returning to the original variable, we finally get:

Example 10. Find integral of a trigonometric function

Solution. Let's change the variable: , then .

Let's transform the integrand to apply the trigonometric identity :

We change the variable, not forgetting to put a minus sign in front of the integral (see above, what is equal to dt). Next, we factor the integrand and integrate according to the table:

Returning to the original variable, we finally get:

Find the integral of a trigonometric function yourself, and then look at the solution

Universal trigonometric substitution

Universal trigonometric substitution can be used in cases where the integrand does not fall under the cases discussed in the previous paragraphs. Basically, when sine or cosine (or both) is in the denominator of a fraction. It has been proven that sine and cosine can be replaced by another expression containing the tangent of half the original angle as follows:

But note that universal trigonometric substitution often entails quite complex algebraic transformations, so it is best used when no other method works. Let us look at examples where, together with the universal trigonometric substitution, substitution under the differential sign and the method of indefinite coefficients are used.

Example 12. Find integral of a trigonometric function

Solution. Solution. Let's take advantage universal trigonometric substitution. Then
.

We multiply the fractions in the numerator and denominator by , and take out the two and place it in front of the integral sign. Then

Examples of solutions of integrals by parts are considered in detail, the integrand of which is the product of a polynomial by an exponential (e to the x power) or by a sine (sin x) or a cosine (cos x).

Content

See also: Method of integration by parts
Table of indefinite integrals
Methods for calculating indefinite integrals
Basic elementary functions and their properties

Formula for integration by parts

When solving examples in this section, the integration by parts formula is used:
;
.

Examples of integrals containing the product of a polynomial and sin x, cos x or e x

Here are examples of such integrals:
, , .

To integrate such integrals, the polynomial is denoted by u, and the remaining part by v dx. Next, apply the integration by parts formula.

Below is a detailed solution to these examples.

Examples of solving integrals

Example with exponent, e to the power of x

Determine the integral:
.

Let us introduce the exponent under the differential sign:
e - x dx = - e - x d(-x) = - d(e - x).

Let's integrate by parts.

Here
.
We also integrate the remaining integral by parts.
.
.
.
Finally we have:
.

An example of defining an integral with sine

Calculate the integral:
.

Let's introduce sine under the differential sign:

Let's integrate by parts.

here u = x 2 , v = cos(2 x+3), du = ( x 2 )′ dx

We also integrate the remaining integral by parts. To do this, introduce the cosine under the differential sign.

here u = x, v = sin(2 x+3), du = dx

Finally we have:

Example of the product of a polynomial and cosine

Calculate the integral:
.

Let's introduce the cosine under the differential sign:

Let's integrate by parts.

here u = x 2 + 3 x + 5, v = sin 2 x, du = ( x 2 + 3 x + 5 )′ dx