Potencijal za kreativnost obično se pripisuje humanističkim naukama, ostavljajući prirodnim naukama analizu, praktičan pristup i suvi jezik formula i brojeva. Matematika se ne može pripisati humanitarnim predmetima. Ali bez kreativnosti u "kraljici svih nauka" nećete ići daleko - ljudi o tome znaju već dugo vremena. Od Pitagorinog vremena, na primjer.
Školski udžbenici, nažalost, obično ne objašnjavaju da je u matematici važno ne samo nagurati teoreme, aksiome i formule. Važno je razumjeti i osjetiti njegove osnovne principe. I u isto vrijeme pokušajte osloboditi svoj um od klišea i elementarnih istina - samo u takvim uvjetima se rađaju sva velika otkrića.
Ova otkrića uključuju ono što danas poznajemo kao Pitagorinu teoremu. Uz nju ćemo pokušati pokazati da matematika ne samo da može, već i treba da bude uzbudljiva. I da ova avantura ne odgovara samo štreberima u debelim naočalama, već i svima koji su jaki umom i jaki duhom.
Iz istorije problema
Strogo govoreći, iako se teorema zove "Pitagorina teorema", sam Pitagora je nije otkrio. Pravokutni trokut i njegova posebna svojstva proučavani su mnogo prije njega. Postoje dva suprotna gledišta o ovom pitanju. Prema jednoj verziji, Pitagora je bio prvi koji je pronašao potpuni dokaz teoreme. Prema drugom, dokaz ne pripada Pitagorinom autorstvu.
Danas ne možete provjeriti ko je u pravu, a ko nije. Poznato je samo da Pitagorin dokaz, ako je ikada postojao, nije preživio. Međutim, postoje sugestije da čuveni dokaz iz Euklidovih "Elemenata" možda pripada Pitagori, a Euklid ga je samo zabilježio.
Danas je također poznato da se problemi oko pravokutnog trougla nalaze u egipatskim izvorima iz vremena faraona Amenemkheta I, na babilonskim glinenim pločama za vrijeme vladavine kralja Hamurabija, u staroindijskoj raspravi "Sulva sutra" i starokineskoj kompozicija "Zhou-bi suan jin".
Kao što vidite, Pitagorina teorema je zaokupljala umove matematičara od davnina. Postoji oko 367 različitih dokaza koji postoje i danas. U tome se nijedna druga teorema ne može takmičiti s njom. Značajni pisci dokaza su Leonardo da Vinci i dvadeseti predsjednik Sjedinjenih Država, James Garfield. Sve ovo govori o izuzetnoj važnosti ove teoreme za matematiku: većina teorema geometrije je izvedena iz nje ili je na ovaj ili onaj način povezana s njom.
Dokaz Pitagorine teoreme
U školskim udžbenicima se uglavnom daju algebarski dokazi. Ali suština teoreme je u geometriji, pa razmotrimo prije svega one dokaze poznate teoreme, koji se temelje na ovoj nauci.
Dokaz 1
Za najjednostavniji dokaz Pitagorine teoreme za pravougli trougao, potrebno je postaviti idealne uslove: neka trougao bude ne samo pravougli, već i jednakokraki. Postoji razlog za vjerovanje da su ovaj trokut prvobitno razmatrali matematičari antike.
Izjava "Kvadrat izgrađen na hipotenuzi pravokutnog trougla jednak je zbiru kvadrata izgrađenih na njegovim kracima" može se ilustrovati sledećim crtežom:
Pogledajte jednakokraki pravougli trougao ABC: Na hipotenuzi AC možete izgraditi kvadrat koji se sastoji od četiri trougla jednaka originalnom ABC. A na kracima AB i BC izgrađen je u kvadratu, od kojih svaki sadrži dva slična trokuta.
Inače, ovaj crtež je bio osnova brojnih anegdota i karikatura posvećenih Pitagorinoj teoremi. Možda je najpoznatiji "Pitagorine pantalone su jednake u svim pravcima":

Dokaz 2
Ova metoda kombinuje algebru i geometriju i može se posmatrati kao varijanta drevnog indijskog dokaza matematičara Bhaskarija.
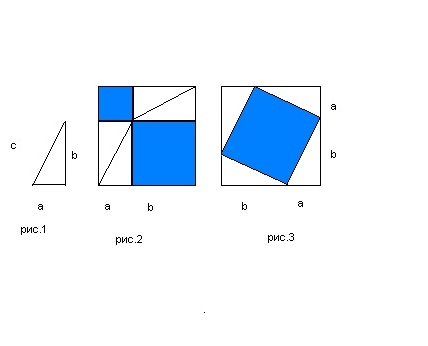
Konstruirajte pravougli trokut sa stranicama a, b i c(sl. 1). Zatim napravite dva kvadrata sa stranicama jednakim zbroju dužina dva kraka, - (a + b)... U svakom od kvadrata konstruirajte kao na slikama 2 i 3.
U prvom kvadratu napravite četiri ista trokuta kao na slici 1. Kao rezultat, dobijate dva kvadrata: jedan sa stranom a, drugi sa stranom b.
U drugom kvadratu četiri slična konstruisana trokuta čine kvadrat sa stranicom jednakom hipotenuzi c.
Zbir površina konstruisanih kvadrata na slici 2 jednak je površini kvadrata koji smo konstruisali sa stranicom c na slici 3. To se lako može provjeriti izračunavanjem površina kvadrata na Sl. 2 po formuli. A površina upisanog kvadrata na slici 3. oduzimanjem površina četiri jednaka upisana u kvadrat pravokutnih trokuta od površine velikog kvadrata sa stranom (a + b).
Zapisujući sve ovo, imamo: a 2 + b 2 = (a + b) 2 - 2ab... Proširite zagrade, izvršite sve potrebne algebarske proračune i dobijete to a 2 + b 2 = a 2 + b 2... U ovom slučaju, područje upisano na sl. 3. kvadrat se može izračunati koristeći tradicionalnu formulu S = c 2... One. a 2 + b 2 = c 2- dokazali ste Pitagorinu teoremu.
Dokaz 3
Isti taj drevni indijski dokaz opisan je u XII veku u raspravi "Kruna znanja" ("Siddhanta Shiromani"), a kao glavni argument autor koristi apel upućen matematičkim talentima i zapažanjima učenika i sledbenika: " Pogledaj!"
Ali ovaj dokaz ćemo detaljnije analizirati:
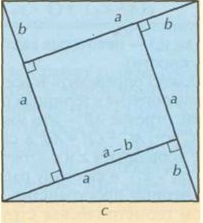
Unutar kvadrata nacrtajte četiri pravokutna trougla kao što je prikazano na crtežu. Strana velikog kvadrata, to je također hipotenuza, označavamo sa... Zovu se katete trougla a i b... Prema crtežu, stranica unutrašnjeg kvadrata je (a-b).
Koristite površinu kvadratne formule S = c 2 za izračunavanje površine vanjskog kvadrata. I u isto vrijeme izračunajte istu vrijednost dodavanjem površine unutrašnjeg kvadrata i površina sva četiri pravokutna trokuta: (a-b) 2 2 + 4 * 1 \ 2 * a * b.
Možete koristiti obje opcije za izračunavanje površine kvadrata kako biste bili sigurni da daju isti rezultat. I to vam daje pravo da to zapišete c 2 = (a-b) 2 + 4 * 1 \ 2 * a * b... Kao rezultat rješenja, dobit ćete formulu Pitagorine teoreme c 2 = a 2 + b 2... Teorema je dokazana.
Dokaz 4
Ovaj čudni drevni kineski dokaz naziva se "Nevjestina stolica" - zbog figure nalik stolici koja se dobija kao rezultat svih konstrukcija:
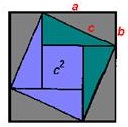
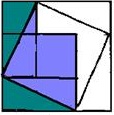
Koristi crtež koji smo već vidjeli na slici 3 u drugom dokazu. A unutrašnji kvadrat sa stranom c je konstruisan na isti način kao u drevnom indijskom dokazu koji je dat gore.
Ako mentalno odrežete dva zelena pravokutna trokuta sa crteža na slici 1, pomaknete ih na suprotne strane kvadrata sa stranom c i hipotenuzama, pričvrstite na hipotenuze lila trokuta, dobićete figuru koja se zove "nevjestina stolica" (Sl. 2). Radi jasnoće, isto možete učiniti s papirnim kvadratima i trokutima. Vidjet ćete da je "mladenkina stolica" formirana od dva kvadrata: malog sa stranom b i veliki sa stranom a.
Ove konstrukcije omogućile su drevnim kineskim matematičarima i nakon njih da dođu do zaključka da c 2 = a 2 + b 2.
Dokaz 5
Ovo je još jedan način za pronalaženje rješenja Pitagorine teoreme, oslanjajući se na geometriju. Zove se Garfildova metoda.
Konstruiši pravougaoni trougao ABC... Moramo to dokazati BC 2 = AC 2 + AB 2.
Da biste to učinili, nastavite nogu AS i nacrtajte segment linije CD koja je jednaka nozi AB... Spustite okomicu AD odjeljak ED... Segmenti ED i AS su jednaki. Povežite tačke E i V, i E i WITH i dobijete crtež kao na slici ispod:
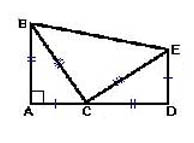
Da bismo dokazali toranj, ponovo pribjegavamo metodi koju smo već isprobali: pronalazimo površinu rezultirajuće figure na dva načina i izjednačavamo izraze jedan s drugim.
Pronađite površinu poligona KREVET moguće je dodavanjem površina tri trougla koji ga čine. i jedan od njih, ERUs, nije samo pravougaona, već i jednakokračna. To takođe ne zaboravljamo AB = CD, AC = ED i BC = CE- ovo će nam omogućiti da pojednostavimo snimanje i ne preopterećujemo ga. dakle, S ABED = 2 * 1/2 (AB * AC) + 1 / 2BC 2.
Štaviše, očigledno je da KREVET Je trapez. Stoga njegovu površinu izračunavamo po formuli: S ABED = (DE + AB) * 1 / 2AD... Za naše proračune je zgodnije i jasnije predstaviti segment AD kao zbir segmenata AS i CD.
Napišimo oba načina za izračunavanje površine figure, stavljajući znak jednakosti između njih: AB * AC + 1 / 2BC 2 = (DE + AB) * 1/2 (AC + CD)... Koristimo jednakost segmenata koji su nam već poznati i gore opisani da pojednostavimo desnu stranu notacije: AB * AC + 1 / 2BC 2 = 1/2 (AB + AC) 2... Sada proširimo zagrade i transformirajmo jednakost: AB * AC + 1 / 2BC 2 = 1 / 2AC 2 + 2 * 1/2 (AB * AC) + 1 / 2AB 2... Nakon završetka svih transformacija, dobijamo upravo ono što nam je potrebno: BC 2 = AC 2 + AB 2... Dokazali smo teoremu.
Naravno, ova lista dokaza je daleko od potpune. Pitagorina teorema se također može dokazati korištenjem vektora, kompleksnih brojeva, diferencijalnih jednadžbi, stereometrije itd. Pa čak i fizika: ako se, na primjer, tekućina izlije u kvadratne i trokutaste zapremine slične onima prikazanim na crtežima. Sipanjem tečnosti može se dokazati jednakost površina i sam teorem kao rezultat.
Nekoliko riječi o Pitagorinim trojkama
Ovo pitanje se malo ili ne proučava u školskom programu. A ipak je vrlo zanimljiv i od velike važnosti u geometriji. Pitagorine trojke se koriste za rješavanje mnogih matematičkih problema. Ideja o njima može vam biti od koristi u daljem školovanju.
Dakle, šta su pitagorine trojke? Ovo je naziv za prirodne brojeve, sakupljene u tri, od kojih je zbir kvadrata dva jednak trećem broju na kvadrat.
Pitagorine trojke mogu biti:
- primitivni (sva tri broja su međusobno prosti);
- nije primitivno (ako se svaki broj trojke pomnoži sa istim brojem, dobićete novu trojku, koja nije primitivna).
Još prije naše ere, stari Egipćani su bili fascinirani manijom broja pitagorejskih trojki: u problemima su razmatrali pravokutni trokut sa stranicama od 3,4 i 5 jedinica. Usput, svaki trougao čije su stranice jednake brojevima iz Pitagorine trojke je pravougaonik po defaultu.
Primjeri pitagorinih trojki: (3, 4, 5), (6, 8, 10), (5, 12, 13), (9, 12, 15), (8, 15, 17), (12, 16, 20) ), (15, 20, 25), (7, 24, 25), (10, 24, 26), (20, 21, 29), (18, 24, 30), (10, 30, 34) ), (21, 28, 35), (12, 35, 37), (15, 36, 39), (24, 32, 40), (9, 40, 41), (27, 36, 45), (14, 48, 50), (30, 40, 50) itd.
Praktična primjena teoreme
Pitagorina teorema nalazi primenu ne samo u matematici, već iu arhitekturi i građevinarstvu, astronomiji, pa čak i književnosti.
Prvo, o konstrukciji: Pitagorina teorema u njoj nalazi široku primenu u problemima različitih nivoa složenosti. Na primjer, pogledajte romanički prozor:
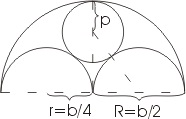
Označimo širinu prozora kao b, tada se radijus polukruga može označiti kao R i izraziti kroz b: R = b / 2... Poluprečnik manjih polukrugova se takođe može izraziti kroz b: r = b / 4... U ovom problemu nas zanima radijus unutrašnjeg kruga prozora (nazovimo ga str).
Pitagorina teorema samo dobro dođe za izračunavanje R... Da bismo to učinili, koristimo pravokutni trokut, koji je na slici označen isprekidanom linijom. Hipotenuza trougla sastoji se od dva poluprečnika: b / 4 + str... Jedna noga je radijus b / 4, druga b / 2-str... Koristeći Pitagorinu teoremu, pišemo: (b / 4 + p) 2 = (b / 4) 2 + (b / 2-p) 2... Zatim otvaramo zagrade i dobivamo b 2/16 + bp / 2 + p 2 = b 2/16 + b 2/4-bp + p 2... Ovaj izraz pretvaramo u bp / 2 = b 2/4-bp... I onda podijelite sve pojmove sa b, dajemo slične za nabavku 3/2 * p = b / 4... I na kraju ćemo to pronaći p = b / 6- što nam je trebalo.
Koristeći teoremu, možete izračunati dužinu rogova za zabatni krov. Odredite koliko je visok mobilni toranj potreban da bi signal stigao do određenog naselja. Čak i trajno postaviti božićno drvce na gradskom trgu. Kao što vidite, ova teorema živi ne samo na stranicama udžbenika, već je često korisna i u stvarnom životu.
Što se tiče književnosti, Pitagorina teorema je inspirisala pisce još od antike i nastavlja da to čini i u naše vreme. Na primjer, njemački pisac iz devetnaestog vijeka Adelbert von Chamisso bio je inspiriran da napiše sonet:
Svetlost istine neće uskoro nestati,
Ali, sijajući, teško da će se raspršiti
I, kao pre milenijuma,
Neće izazvati sumnje i sporove.
Najmudriji kada dotakne oko
Svetlost istine, zahvaljujući bogovima;
I sto bikova, izbodenih, lažu -
Uzvratni poklon od srećnog Pitagore.
Od tada bikovi očajnički urlaju:
Zauvijek uznemiren plemenom bikova
Događaj koji se ovdje spominje.
Čini im se: dolazi vrijeme
I opet će biti žrtvovani
Neka sjajna teorema.
(prevod Viktor Toporov)
A u dvadesetom veku, sovjetski pisac Jevgenij Veltistov posvetio je čitavo poglavlje dokazu Pitagorine teoreme u svojoj knjizi "Avanture elektronike". I još pola poglavlja priče o dvodimenzionalnom svijetu, koji bi mogao postojati kada bi Pitagorina teorema postala temeljni zakon, pa čak i religija za jedan svijet. U njemu bi bilo mnogo lakše živjeti, ali i mnogo dosadnije: na primjer, tamo niko ne razumije značenje riječi "okrugla" i "puhasto".
A u knjizi "Avanture elektronike" autor, kroz usta nastavnika matematike Taratara, kaže: "Glavna stvar u matematici je kretanje misli, novih ideja." Upravo taj kreativni let misli dovodi do Pitagorine teoreme - nema zaluda da ima toliko različitih dokaza. Pomaže da se izađe izvan granica poznatog i da se na poznate stvari sagleda na novi način.
Zaključak
Ovaj članak je kreiran kako biste mogli pogledati dalje od školskog nastavnog plana i programa iz matematike i saznati ne samo dokaze Pitagorine teoreme, koji su dati u udžbenicima "Geometrija 7-9" (L. S. Atanasyan, V. N. Rudenko) i "Geometrija 7 -11“ (AV Pogorelov), ali i druge radoznale načine dokazivanja čuvene teoreme. I također pogledajte primjere kako se Pitagorina teorema može primijeniti u svakodnevnom životu.
Prvo, ove informacije će vam omogućiti da se kvalificirate za više ocjene na časovima matematike - informacije o toj temi iz dodatnih izvora su uvijek visoko cijenjene.
Drugo, željeli smo da vam pomognemo da steknete utisak koliko je matematika zanimljiva. Uvjerite se konkretnim primjerima da u tome uvijek ima mjesta za kreativnost. Nadamo se da će Pitagorina teorema i ovaj članak inspirisati vaše samostalno istraživanje i uzbudljiva otkrića u matematici i drugim naukama.
Recite nam u komentarima da li su vam dokazi u ovom članku bili zanimljivi. Da li vam je ova informacija bila korisna tokom studija? Napišite nam šta mislite o Pitagorinoj teoremi i ovom članku - biće nam zadovoljstvo da o svemu tome razgovaramo s vama.
blog.site, uz potpuno ili djelomično kopiranje materijala, obavezan je link na izvor.