Potenciál pro kreativitu je obvykle připisován humanitním vědám, přírodním vědám zůstává analýza, praktický přístup a suchý jazyk vzorců a čísel. Matematiku nelze přiřadit k humanitním předmětům. Ale bez kreativity v "královně všech věd" daleko nedojdete - lidé o tom vědí už dlouho. Například od dob Pythagora.
Školní učebnice bohužel většinou nevysvětlují, že v matematice je důležité nejen nacpat věty, axiomy a vzorce. Je důležité pochopit a cítit jeho základní principy. A zároveň se snažte osvobodit svou mysl od klišé a elementárních pravd – jen v takových podmínkách se rodí všechny velké objevy.
Tyto objevy zahrnují to, co dnes známe jako Pythagorovu větu. S jeho pomocí se pokusíme ukázat, že matematika nejen umí, ale má být vzrušující. A že toto dobrodružství je vhodné nejen pro nerdy v tlustých brýlích, ale pro všechny, kdo jsou silní myslí a silní duchem.
Z historie vydání
Přísně vzato, ačkoli se věta nazývá „Pythagorova věta“, sám Pythagoras ji neobjevil. Pravoúhlý trojúhelník a jeho speciální vlastnosti byly studovány dávno před ním. Na tuto problematiku existují dva protichůdné pohledy. Podle jedné verze byl Pythagoras první, kdo našel úplný důkaz teorému. Podle jiného důkaz nepatří k autorství Pythagora.
Dnes nemůžete zkontrolovat, kdo má pravdu a kdo se mýlí. Ví se pouze, že důkaz o Pythagorovi, pokud vůbec existoval, se nedochoval. Existují však návrhy, že slavný důkaz z Euklidových „Prvků“ může patřit Pythagorovi a Euklides jej pouze zaznamenal.
Dnes je také známo, že problémy s pravoúhlým trojúhelníkem se nacházejí v egyptských pramenech z doby faraona Amenemcheta I., na babylonských hliněných tabulkách za vlády krále Hammurabiho, ve starověkém indickém pojednání „Sulva sútra“ a ve starých čínských skladba "Zhou-bi suan jin".
Jak vidíte, Pythagorova věta zaměstnávala mysl matematiků již od starověku. I dnes existuje asi 367 různých důkazů. V tomto jí žádná jiná věta nemůže konkurovat. Mezi významné autory korektur patří Leonardo da Vinci a dvacátý prezident Spojených států James Garfield. To vše hovoří o mimořádné důležitosti této věty pro matematiku: většina vět o geometrii je z ní odvozena nebo s ní tak či onak souvisí.
Důkaz Pythagorovy věty
Ve školních učebnicích jsou uváděny převážně algebraické důkazy. Ale podstata teorému je v geometrii, takže uvažujme nejprve o těch důkazech slavné věty, které jsou založeny na této vědě.
Důkaz 1
Pro nejjednodušší důkaz Pythagorovy věty pro pravoúhlý trojúhelník je potřeba nastavit ideální podmínky: ať je trojúhelník nejen pravoúhlý, ale i rovnoramenný. Existuje důvod se domnívat, že tento trojúhelník byl původně zvažován matematiky starověku.
Tvrzení "Čtverec postavený na přeponě pravoúhlého trojúhelníku se rovná součtu čtverců postavených na jeho nohách." lze ilustrovat následujícím nákresem:
Podívejte se na rovnoramenný pravoúhlý trojúhelník ABC: Na přeponě AC můžete postavit čtverec sestávající ze čtyř trojúhelníků rovných původnímu ABC. A na nohách AB a BC je postaven do čtverce, z nichž každý obsahuje dva podobné trojúhelníky.
Mimochodem, tato kresba tvořila základ mnoha anekdot a karikatur věnovaných Pythagorově větě. Snad nejznámější je "Pythagorejské kalhoty jsou stejné ve všech směrech":

Důkaz 2
Tato metoda kombinuje algebru a geometrii a lze ji považovat za variantu staroindického důkazu matematika Bhaskariho.
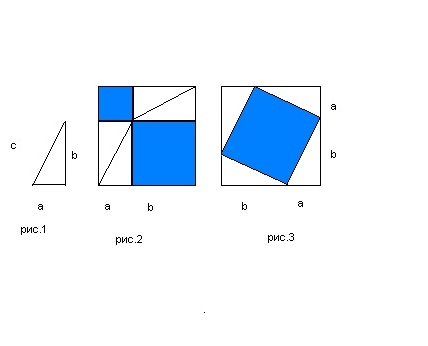
Sestrojte pravoúhlý trojúhelník se stranami a, b a c(Obr. 1). Poté postavte dva čtverce se stranami rovnými součtu délek obou nohou, - (a + b)... V každém ze čtverců sestrojte jako na obrázcích 2 a 3.
V prvním čtverci postavte čtyři stejné trojúhelníky jako na obrázku 1. Výsledkem jsou dva čtverce: jeden se stranou a, druhý se stranou b.
Ve druhém čtverci tvoří čtyři podobné sestrojené trojúhelníky čtverec se stranou rovnou přeponě C.
Součet ploch sestrojených čtverců na obr. 2 se rovná ploše čtverce, kterou jsme sestrojili se stranou c na obr. 3. To lze snadno ověřit výpočtem ploch čtverců na Obr. 2 podle vzorce. A plocha vepsaného čtverce na obrázku 3. odečtením ploch čtyř stejných vepsaných do čtverce pravoúhlých trojúhelníků od plochy velkého čtverce se stranou (a + b).
Když si to všechno zapíšeme, máme: a 2 + b 2 = (a + b) 2 - 2ab... Rozbalte závorky, proveďte všechny potřebné algebraické výpočty a získejte to a 2 + b 2 = a 2 + b 2... V tomto případě oblast napsaná na obr. 3. čtverec lze vypočítat pomocí tradičního vzorce S = c 2... Tito. a 2 + b 2 = c 2- dokázal jsi Pythagorovu větu.
Důkaz 3
Tentýž starověký indický důkaz je popsán v 12. století v pojednání „Koruna vědění“ („Siddhanta Shiromani“) a jako hlavní argument autor používá výzvu adresovanou matematickým talentům a pozorování studentů a následovníků: „ Koukni se!"
Tento důkaz však rozebereme podrobněji:
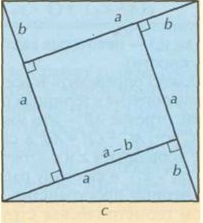
Uvnitř čtverce nakreslete čtyři pravoúhlé trojúhelníky, jak je naznačeno na obrázku. Stranu velkého čtverce, to je také přepona, označujeme s... Nohy trojúhelníku se nazývají A a b... Strana vnitřního čtverce je dle nákresu (a-b).
Použijte plochu čtvercového vzorce S = c 2 pro výpočet plochy vnějšího čtverce. A zároveň vypočítejte stejnou hodnotu sečtením plochy vnitřního čtverce a ploch všech čtyř pravoúhlých trojúhelníků: (a-b) 2 2 + 4 * 1 \ 2 * a * b.
Pro výpočet plochy čtverce můžete použít obě možnosti, abyste se ujistili, že dávají stejný výsledek. A to vám dává právo to napsat c 2 = (a-b) 2 + 4 * 1 \ 2 * a * b... V důsledku řešení získáte vzorec Pythagorovy věty c 2 = a 2 + b 2... Věta je dokázána.
Důkaz 4
Tento podivný starověký čínský důkaz se nazývá „křeslo nevěsty“ - kvůli postavě podobné židli, která je výsledkem všech konstrukcí:
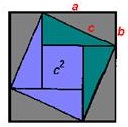
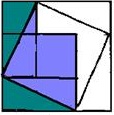
Využívá kresbu, kterou jsme již viděli na obrázku 3 ve druhém důkazu. A vnitřní čtverec se stranou c je konstruován stejným způsobem jako ve starověkém indickém důkazu uvedeném výše.
Pokud v duchu odříznete dva zelené pravoúhlé trojúhelníky z výkresu na obr. 1, přemístíte je na opačné strany čtverce se stranou c a přeponami, připojíte k přeponám lila trojúhelníků, získáte postavu zvanou "křeslo nevěsty" (obr. 2). Pro přehlednost můžete udělat totéž s papírovými čtverci a trojúhelníky. Uvidíte, že "křeslo nevěsty" je tvořeno dvěma čtverci: malým se stranou b a velký s bokem A.
Tyto konstrukce umožnily starým čínským matematikům a po nich dojít k závěru, že c 2 = a 2 + b 2.
Důkaz 5
Toto je další způsob, jak najít řešení Pythagorovy věty, opírající se o geometrii. Říká se tomu Garfieldova metoda.
Sestrojte pravoúhlý trojúhelník ABC... Musíme to dokázat BC 2 = AC 2 + AB 2.
Chcete-li to provést, pokračujte v noze TAK JAKO a nakreslete úsečku CD která se rovná noze AB... Snižte kolmici INZERÁT sekce ED... Segmenty ED a TAK JAKO jsou si rovni. Spojit tečky E a PROTI, a E a S a získejte výkres jako na obrázku níže:
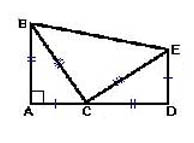
Abychom věž dokázali, znovu se uchýlíme k metodě, kterou jsme již vyzkoušeli: najděte plochu výsledné postavy dvěma způsoby a přirovnejte výrazy k sobě navzájem.
Najděte oblast mnohoúhelníku POSTEL je to možné sečtením oblastí tří trojúhelníků, které jej tvoří. A jeden z nich, ERU, je nejen pravoúhlý, ale i rovnoramenný. Na to také nezapomínáme AB = CD, AC = ED a BC = CE- to nám umožní zjednodušit záznam a nepřetěžovat jej. Tak, S ABED = 2 * 1/2 (AB * AC) + 1 / 2 BC 2.
Navíc je zřejmé, že POSTEL Je lichoběžník. Jeho plochu tedy vypočítáme podle vzorce: S ABED = (DE + AB) * 1 / 2AD... Pro naše výpočty je pohodlnější a přehlednější reprezentovat segment INZERÁT jako součet segmentů TAK JAKO a CD.
Pojďme napsat oba způsoby, jak vypočítat plochu obrázku, přičemž mezi ně vložíme rovnítko: AB * AC + 1 / 2BC 2 = (DE + AB) * 1/2 (AC + CD)... Pro zjednodušení pravé strany zápisu používáme rovnost segmentů, které již známe a jsou popsány výše: AB * AC + 1 / 2BC 2 = 1/2 (AB + AC) 2... Nyní rozbalme závorky a transformujme rovnost: AB * AC + 1 / 2BC 2 = 1 / 2AC 2 + 2 * 1/2 (AB * AC) + 1 / 2AB 2... Po dokončení všech transformací dostaneme přesně to, co potřebujeme: BC 2 = AC 2 + AB 2... Větu jsme dokázali.
Tento výčet důkazů samozřejmě není zdaleka úplný. Pythagorovu větu lze také dokázat pomocí vektorů, komplexních čísel, diferenciálních rovnic, stereometrie atd. A dokonce i fyzika: pokud se například kapalina nalije do čtvercových a trojúhelníkových objemů podobných těm, které jsou znázorněny na výkresech. Naléváním kapaliny lze dokázat rovnost ploch a jako výsledek samotnou větu.
Pár slov o pythagorejských trojicích
Tato problematika je ve školních osnovách málo probírána nebo není studována. A přesto je velmi zajímavý a má velký význam v geometrii. Pythagorejské trojice se používají k řešení mnoha matematických problémů. Myšlenka na ně se vám může hodit při vašem dalším vzdělávání.
Co jsou tedy pythagorejská trojčata? Toto je název pro přirozená čísla, shromážděná ve třech, přičemž součet druhých mocnin z nichž se rovná třetímu číslu na druhou.
Pythagorejské trojice mohou být:
- primitivní (všechna tři čísla jsou vzájemně prvočísla);
- není primitivní (pokud je každé číslo trojky vynásobeno stejným číslem, dostanete novou trojku, která není primitivní).
Již před naším letopočtem byli staří Egypťané fascinováni mánií počtu pythagorejských trojic: v úlohách uvažovali o pravoúhlém trojúhelníku o stranách 3,4 a 5 jednotek. Mimochodem, každý trojúhelník, jehož strany se rovnají číslům z pythagorejské trojice, je ve výchozím nastavení obdélníkový.
Příklady pythagorejských trojic: (3, 4, 5), (6, 8, 10), (5, 12, 13), (9, 12, 15), (8, 15, 17), (12, 16, 20) ), (15, 20, 25), (7, 24, 25), (10, 24, 26), (20, 21, 29), (18, 24, 30), (10, 30, 34 ), (21, 28, 35), (12, 35, 37), (15, 36, 39), (24, 32, 40), (9, 40, 41), (27, 36, 45), (14, 48, 50), (30, 40, 50) atd.
Praktická aplikace věty
Pythagorova věta nachází uplatnění nejen v matematice, ale také v architektuře a stavebnictví, astronomii a dokonce i v literatuře.
Nejprve o konstrukci: Pythagorova věta v ní nachází široké uplatnění v problémech různé úrovně složitosti. Podívejte se například na románské okno:
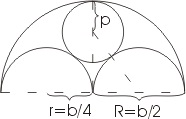
Označme šířku okna jako b, pak lze poloměr půlkruhu označit jako R a vyjádřit prostřednictvím b: R = b/2... Poloměr menších půlkruhů může být také vyjádřen skrz b: r = b / 4... V tomto problému nás zajímá poloměr vnitřního kruhu okna (říkejme tomu p).
K výpočtu se prostě hodí Pythagorova věta R... K tomu nám slouží pravoúhlý trojúhelník, který je na obrázku naznačen tečkovanou čarou. Přepona trojúhelníku se skládá ze dvou poloměrů: b / 4 + str... Jedna noha je poloměr b/4, další b / 2-p... Pomocí Pythagorovy věty píšeme: (b / 4 + p) 2 = (b / 4) 2 + (b / 2-p) 2... Dále otevřeme závorky a dostaneme b 2/16 + bp / 2 + p 2 = b 2/16 + b 2/4-bp + p 2... Tento výraz transformujeme na bp/2 = b 2/4-bp... A pak vydělte všechny termíny podle b, podobné dáváme k získání 3/2 * p = b / 4... A to nakonec najdeme p = b / 6- což jsme potřebovali.
Pomocí věty můžete vypočítat délku krokví pro sedlovou střechu. Určete, jak vysoká je mobilní věž potřebná k tomu, aby signál dosáhl určité osady. A dokonce natrvalo postavit vánoční strom na náměstí. Jak je vidět, tato věta žije nejen na stránkách učebnic, ale často se hodí i v reálném životě.
Pokud jde o literaturu, Pythagorova věta inspirovala spisovatele již od starověku a pokračuje v tom i v naší době. Například německý spisovatel devatenáctého století Adelbert von Chamisso byl inspirován k napsání sonetu:
Světlo pravdy se brzy nerozplyne,
Ale svítí, jen stěží se rozplyne
A jako před tisíciletími
Nevyvolává pochybnosti a spory.
Nejmoudřejší, když se dotkne oka
Světlo pravdy, díky bohům;
A sto býků, pobodaných, lež -
Vzájemný dárek od šťastného Pythagora.
Od té doby býci zoufale řvou:
Navždy znepokojený býčím kmenem
Zde zmíněná událost.
Zdá se jim: čas se blíží
A znovu budou obětováni
Nějaká velká věta.
(překlad Viktor Toporov)
A ve dvacátém století věnoval sovětský spisovatel Jevgenij Veltistov ve své knize „Dobrodružství elektroniky“ celou kapitolu důkazu Pythagorovy věty. A ještě půl kapitoly k příběhu o dvourozměrném světě, který by mohl existovat, kdyby se Pythagorova věta stala základním zákonem a dokonce náboženstvím pro jeden svět. Žilo by se v něm mnohem snáz, ale také mnohem nudněji: nikdo tam například nechápe význam slov „kulatý“ a „načechraný“.
A v knize "The Adventures of Electronics" autor ústy učitele matematiky Taratar říká: "Hlavní věcí v matematice je pohyb myšlení, nové myšlenky." Právě tento tvůrčí myšlenkový let dává vzniknout Pythagorově větě – ne nadarmo má tolik různých důkazů. Pomáhá překročit hranice známého a podívat se na známé věci novým způsobem.
Závěr
Tento článek vznikl proto, abyste nahlédli za hranice školního učiva v matematice a zjistili nejen důkazy Pythagorovy věty, které jsou uvedeny v učebnicích „Geometrie 7-9“ (L. S. Atanasyan, V. N. Rudenko) a „Geometrie 7 -11“ (AV Pogorelov), ale také další kuriózní způsoby, jak dokázat slavnou větu. A také se podívejte na příklady, jak lze Pythagorovu větu aplikovat v běžném životě.
Za prvé, tyto informace vám umožní kvalifikovat se na vyšší skóre v hodinách matematiky – informace o tématu z dalších zdrojů jsou vždy vysoce ceněny.
Za druhé, chtěli jsme vám pomoci získat představu o tom, jak zajímavá matematika je. Ujistěte se na konkrétních příkladech, že v ní je vždy místo pro kreativitu. Doufáme, že Pythagorova věta a tento článek budou inspirací pro vaše nezávislé bádání a vzrušující objevy v matematice a dalších vědách.
Řekněte nám v komentářích, zda vás důkazy v tomto článku zaujaly. Byly pro vás tyto informace užitečné při vašem studiu? Napište nám, co si myslíte o Pythagorově větě a tomto článku – rádi s vámi o tom všem budeme diskutovat.
blog. s úplným nebo částečným zkopírováním materiálu, je vyžadován odkaz na zdroj.