Potencjał kreatywności przypisuje się zwykle naukom humanistycznym, pozostawiając naukom przyrodniczym analizę, praktyczne podejście i suchy język formuł i liczb. Matematyki nie można przypisać przedmiotom humanitarnym. Ale bez kreatywności w "królowej wszystkich nauk" daleko nie zajdziesz - ludzie wiedzieli o tym od dawna. Na przykład od czasów Pitagorasa.
Podręczniki szkolne niestety zwykle nie wyjaśniają, że w matematyce ważne jest nie tylko wkuwanie twierdzeń, aksjomatów i formuł. Ważne jest, aby zrozumieć i poczuć jego podstawowe zasady. A jednocześnie staraj się uwolnić swój umysł od frazesów i elementarnych prawd – tylko w takich warunkach rodzą się wszystkie wielkie odkrycia.
Odkrycia te obejmują to, co znamy dzisiaj jako twierdzenie Pitagorasa. Z jego pomocą postaramy się pokazać, że matematyka nie tylko może, ale powinna być ekscytująca. I że ta przygoda jest odpowiednia nie tylko dla nerdów w grubych okularach, ale dla każdego, kto jest silny w umyśle i silny duchem.
Z historii problemu
Ściśle mówiąc, chociaż twierdzenie to nazywa się „twierdzeniem Pitagorasa”, sam Pitagoras go nie odkrył. Trójkąt prostokątny i jego szczególne właściwości badano na długo przed nim. W tej kwestii istnieją dwa przeciwstawne punkty widzenia. Według jednej wersji Pitagoras jako pierwszy znalazł kompletny dowód twierdzenia. Według innego dowód nie należy do autorstwa Pitagorasa.
Dziś nie można sprawdzić, kto ma rację, a kto się myli. Wiadomo tylko, że dowód Pitagorasa, jeśli kiedykolwiek istniał, nie przetrwał. Jednakże istnieją sugestie, że słynny dowód z „Elementów” Euklidesa może należeć do Pitagorasa, a Euklides tylko go zapisał.
Wiadomo również dzisiaj, że problemy dotyczące trójkąta prostokątnego znajdują się w egipskich źródłach z czasów faraona Amenemhata I, na babilońskich tabliczkach glinianych z okresu panowania króla Hammurabiego, w starożytnym indyjskim traktacie „Sulva sutra” i starożytna chińska kompozycja „Zhou-bi suan jin”.
Jak widać, twierdzenie Pitagorasa od czasów starożytnych zajmowało umysły matematyków. Istnieje również około 367 różnych dowodów. Pod tym względem żadne inne twierdzenie nie może z nim konkurować. Znani autorzy dowodów to Leonardo da Vinci i dwudziesty prezydent Stanów Zjednoczonych, James Garfield. Wszystko to świadczy o ogromnym znaczeniu tego twierdzenia dla matematyki: większość twierdzeń geometrii wywodzi się z niego lub w ten czy inny sposób jest z nim związany.
Dowód twierdzenia Pitagorasa
W podręcznikach szkolnych podaje się głównie dowody algebraiczne. Ale istota twierdzenia tkwi w geometrii, więc rozważmy przede wszystkim te dowody słynnego twierdzenia, które opierają się na tej nauce.
Dowód 1
Aby uzyskać najprostszy dowód twierdzenia Pitagorasa dla trójkąta prostokątnego, musisz ustawić idealne warunki: niech trójkąt będzie nie tylko prostokątny, ale także równoramienny. Istnieją powody, by sądzić, że trójkąt ten był pierwotnie rozważany przez matematyków starożytności.
Oświadczenie "Kwadrat zbudowany na przeciwprostokątnej trójkąta prostokątnego jest równy sumie kwadratów zbudowanych na jego nogach" można zilustrować następującym rysunkiem:
Spójrz na trójkąt równoramienny ABC: Na przeciwprostokątnej AC możesz zbudować kwadrat składający się z czterech trójkątów równych pierwotnemu ABC. A na nogach AB i BC jest zbudowany w kwadracie, z których każdy zawiera dwa podobne trójkąty.
Nawiasem mówiąc, ten rysunek był podstawą wielu anegdot i karykatur poświęconych twierdzeniu Pitagorasa. Najbardziej znanym jest być może „Pitagorejskie spodnie są jednakowe we wszystkich kierunkach”:

Dowód 2
Ta metoda łączy algebrę i geometrię i może być postrzegana jako wariant starożytnego indyjskiego dowodu matematyka Bhaskari.
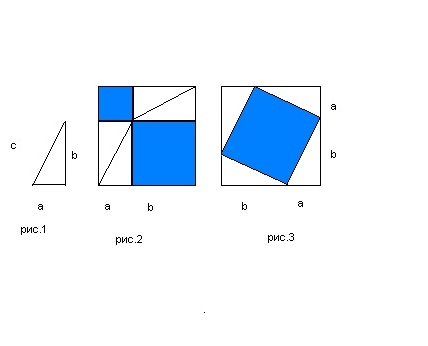
Skonstruuj trójkąt prostokątny z bokami a, b i c(rys. 1). Następnie zbuduj dwa kwadraty o bokach równych sumie długości dwóch nóg, - (a + b)... W każdym z kwadratów skonstruuj jak na rysunkach 2 i 3.
W pierwszym kwadracie zbuduj cztery takie same trójkąty, jak na rysunku 1. W rezultacie otrzymasz dwa kwadraty: jeden o boku a, drugi o boku b.
W drugim kwadracie cztery podobne do siebie trójkąty tworzą kwadrat o boku równym przeciwprostokątnej C.
Suma pól zbudowanych kwadratów na ryc. 2 jest równa powierzchni kwadratu, który zbudowaliśmy o boku c na ryc. 3. Można to łatwo zweryfikować, obliczając pola kwadratów na ryc. 2 według wzoru. A obszar kwadratu wpisanego na ryc. 3. odejmując obszary czterech równych wpisanych w kwadrat trójkąty prostokątne od obszaru dużego kwadratu z bokiem (a + b).
Zapisując to wszystko mamy: a 2 + b 2 = (a + b) 2 - 2ab... Rozwiń nawiasy, wykonaj wszystkie niezbędne obliczenia algebraiczne i zdobądź to a 2 + b 2 = a 2 + b 2... W tym przypadku obszar wpisany na rys. 3. kwadrat można obliczyć za pomocą tradycyjnego wzoru S = c 2... Te. a 2 + b 2 = c 2- udowodniłeś twierdzenie Pitagorasa.
Dowód 3
Ten sam starożytny dowód indyjski jest opisany w XII wieku w traktacie „Korona wiedzy” („Siddhanta Shiromani”) i jako główny argument autor używa apelu skierowanego do talentów matematycznych i obserwacji uczniów i wyznawców: „ Wyglądać!"
Ale przeanalizujemy ten dowód bardziej szczegółowo:
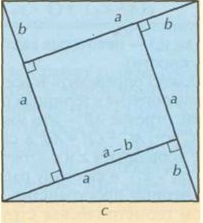
Wewnątrz kwadratu narysuj cztery trójkąty prostokątne, jak pokazano na rysunku. Bok dużego kwadratu jest również przeciwprostokątną, oznaczamy z... Nogi trójkąta nazywane są a oraz b... Zgodnie z rysunkiem, bok wewnętrznego kwadratu to (a-b).
Użyj pola kwadratowego wzoru S = c 2 obliczyć powierzchnię zewnętrznego kwadratu. Jednocześnie oblicz tę samą wartość, dodając obszar wewnętrznego kwadratu i obszary wszystkich czterech trójkątów prostokątnych: (a-b) 2 2 + 4 * 1 \ 2 * a * b.
Możesz użyć obu opcji do obliczenia powierzchni kwadratu, aby upewnić się, że dają ten sam wynik. A to daje ci prawo do zapisania tego c 2 = (a-b) 2 + 4 * 1 \ 2 * a * b... W wyniku rozwiązania otrzymasz wzór twierdzenia Pitagorasa c 2 = a 2 + b 2... Twierdzenie jest udowodnione.
Dowód 4
Ten ciekawy starożytny chiński dowód nazywa się "Krzesłem Panny Młodej" - z powodu podobnej do krzesła figury, która jest uzyskiwana w wyniku wszystkich konstrukcji:
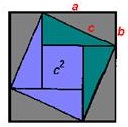
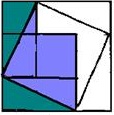
Wykorzystuje rysunek, który już widzieliśmy na rysunku 3 w drugim dowodzie. A wewnętrzny kwadrat o boku c jest skonstruowany w taki sam sposób, jak w podanym powyżej starożytnym indyjskim dowodzie.
Jeśli odetniesz w myślach dwa zielone trójkąty prostokątne z rysunku na ryc. 1, przesuniesz je na przeciwległe boki kwadratu bokiem c i przeciwprostokątnymi, przymocujesz do przeciwprostokątnych trójkątów liliowych, otrzymasz figurę zwaną „krzesłem panny młodej " (ryc. 2). Dla jasności możesz zrobić to samo z papierowymi kwadratami i trójkątami. Zobaczysz, że „krzesło panny młodej” tworzą dwa kwadraty: mały z bokiem b i duże z boku a.
Konstrukcje te pozwoliły starożytnym chińskim matematykom, a my podążając za nimi dojść do wniosku, że c 2 = a 2 + b 2.
Dowód 5
To kolejny sposób na znalezienie rozwiązania twierdzenia Pitagorasa, opierając się na geometrii. Nazywa się metoda Garfielda.
Skonstruuj trójkąt prostokątny ABC... Musimy to udowodnić BC2 = AC2 + AB2.
Aby to zrobić, kontynuuj nogę JAK i narysuj segment Płyta CD która jest równa nodze AB... Opuść prostopadły OGŁOSZENIE Sekcja ED... Segmenty ED oraz JAK są równe. Połącz kropki mi oraz V, oraz mi oraz Z i zdobądź rysunek jak na poniższym obrazku:
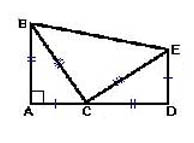
Aby udowodnić wieżę, ponownie stosujemy metodę, którą już wypróbowaliśmy: znajdź obszar wynikowej figury na dwa sposoby i zrównaj wyrażenia ze sobą.
Znajdź obszar wielokąta ŁÓŻKO jest to możliwe przez dodanie obszarów trzech trójkątów, które go tworzą. A jeden z nich, Jednostki ERU, jest nie tylko prostokątny, ale także równoramienny. O tym też nie zapominamy AB = CD, AC = ED oraz BC = CE- pozwoli nam to uprościć nagranie i nie przeciążać go. Więc, S ABED = 2 * 1/2 (AB * AC) + 1 / 2BC 2.
Co więcej, oczywiste jest, że ŁÓŻKO Czy trapez. Dlatego obliczamy jego powierzchnię według wzoru: S ABED = (DE + AB) * 1 / 2AD... Dla naszych obliczeń wygodniej i wyraźniej jest reprezentować segment OGŁOSZENIE jako suma odcinków JAK oraz Płyta CD.
Napiszmy oba sposoby obliczania powierzchni figury, umieszczając między nimi znak równości: AB * AC + 1/2BC 2 = (DE + AB) * 1/2 (AC + CD)... Używamy równości segmentów już nam znanej i opisanej powyżej, aby uprościć prawą stronę notacji: AB * AC + 1/2BC 2 = 1/2 (AB + AC) 2... Teraz rozszerzmy nawiasy i przekształćmy równość: AB * AC + 1/2BC 2 = 1/2 AC 2 + 2 * 1/2 (AB * AC) + 1/2 AB 2... Po wykonaniu wszystkich transformacji otrzymujemy dokładnie to, czego potrzebujemy: BC2 = AC2 + AB2... Udowodniliśmy twierdzenie.
Oczywiście ta lista dowodów nie jest kompletna. Twierdzenie Pitagorasa można również udowodnić za pomocą wektorów, liczb zespolonych, równań różniczkowych, stereometrii itp. A nawet fizyka: jeśli np. płyn wleje się do kwadratowych i trójkątnych objętości podobnych do tych pokazanych na rysunkach. Wlewając płyn, można w rezultacie udowodnić równość pól i samego twierdzenia.
Kilka słów o trójkach pitagorejskich
Ta kwestia jest mało lub nie jest badana w szkolnym programie nauczania. A jednak jest bardzo ciekawa i ma duże znaczenie w geometrii. Trójki pitagorejskie służą do rozwiązywania wielu problemów matematycznych. Ich pomysł może Ci się przydać w dalszej edukacji.
Czym więc są trójki pitagorejskie? Jest to nazwa liczb naturalnych zebranych w trzy, których suma kwadratów dwóch jest równa trzeciej liczbie do kwadratu.
Trojaczki pitagorejskie mogą być:
- prymitywne (wszystkie trzy liczby są wzajemnie pierwsze);
- nie prymitywne (jeśli każda liczba trójki jest pomnożona przez tę samą liczbę, otrzymujesz nową trójkę, która nie jest pierwotna).
Jeszcze przed naszą erą starożytni Egipcjanie byli zafascynowani manią liczby trojaczków pitagorejskich: w problemach uważali trójkąt prostokątny o bokach 3,4 i 5 jednostek. Nawiasem mówiąc, każdy trójkąt, którego boki są równe liczbom z trójki pitagorejskiej, jest domyślnie prostokątny.
Przykłady trójek pitagorejskich: (3, 4, 5), (6, 8, 10), (5, 12, 13), (9, 12, 15), (8, 15, 17), (12, 16, 20) ), (15, 20, 25), (7, 24, 25), (10, 24, 26), (20, 21, 29), (18, 24, 30), (10, 30, 34 ), (21, 28, 35), (12, 35, 37), (15, 36, 39), (24, 32, 40), (9, 40, 41), (27, 36, 45), (14 , 48, 50), (30, 40, 50) itd.
Praktyczne zastosowanie twierdzenia
Twierdzenie Pitagorasa znajduje zastosowanie nie tylko w matematyce, ale także w architekturze i budownictwie, astronomii, a nawet literaturze.
Po pierwsze, o konstrukcji: twierdzenie Pitagorasa znajduje w nim szerokie zastosowanie w problemach o różnym stopniu złożoności. Na przykład spójrz na okno romańskie:
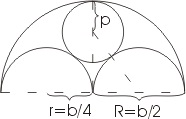
Oznaczmy szerokość okna jako b, to promień półokręgu można oznaczyć jako r i wyrazić przez b: R = b / 2... Promień mniejszych półokręgów można również wyrazić za pomocą b: r = b / 4... W tym problemie interesuje nas promień wewnętrznego okręgu okna (nazwijmy to P).
Twierdzenie Pitagorasa po prostu przydaje się do obliczenia r... Aby to zrobić, używamy trójkąta prostokątnego, który jest oznaczony na rysunku linią przerywaną. Przeciwprostokątna trójkąta składa się z dwóch promieni: b / 4 + p... Jedna noga to promień b / 4, inne b / 2-p... Korzystając z twierdzenia Pitagorasa piszemy: (b / 4 + p) 2 = (b / 4) 2 + (b / 2-p) 2... Następnie otwieramy nawiasy i dostajemy b 2/16 + bp / 2 + p 2 = b 2/16 + b 2/4-bp + p 2... Przekształcamy to wyrażenie w bp / 2 = b 2/4-bp... A następnie dzielimy wszystkie terminy przez b, dajemy podobne do zdobycia 3/2 * p = b / 4... I w końcu to odkryjemy p = b / 6- czego potrzebowaliśmy.
Korzystając z twierdzenia, możesz obliczyć długość krokwi dla dachu dwuspadowego. Określ, jak wysoka jest wieża mobilna, aby sygnał dotarł do określonej osady. A nawet postawić na stałe choinkę na rynku. Jak widać, twierdzenie to żyje nie tylko na kartach podręczników, ale często jest przydatne w prawdziwym życiu.
Jeśli chodzi o literaturę, twierdzenie Pitagorasa inspirowało pisarzy od starożytności i nadal to robi w naszych czasach. Na przykład XIX-wieczny pisarz niemiecki Adelbert von Chamisso został zainspirowany do napisania sonetu:
Światło prawdy wkrótce nie zgaśnie,
Ale świecąc, prawie się nie rozproszy
I, jak tysiące lat temu,
Nie spowoduje wątpliwości i sporów.
Najmądrzejszy, gdy dotyka oka
Światło prawdy, bogom dziękuje się;
I sto byków, dźgniętych, kłamie -
Wzajemny prezent od szczęśliwego Pitagorasa.
Od tego czasu byki rozpaczliwie ryczą:
Na zawsze zaalarmowany plemieniem byków
Wspomniane tutaj wydarzenie.
Wydaje im się: nadchodzi czas
I znowu będą ofiarowani
Wielkie twierdzenie.
(tłumaczenie Wiktora Toporowa)
A w XX wieku radziecki pisarz Jewgienij Veltistow w swojej książce „Przygody elektroniki” poświęcił cały rozdział dowodowi twierdzenia Pitagorasa. I pół rozdziału więcej do historii dwuwymiarowego świata, który mógłby istnieć, gdyby twierdzenie Pitagorasa stało się podstawowym prawem, a nawet religią dla jednego świata. Byłoby o wiele łatwiej w nim żyć, ale też o wiele nudniej: na przykład nikt nie rozumie znaczenia słów „okrągły” i „puszysty”.
A w książce „Przygody elektroniki” autor ustami nauczyciela matematyki Taratara mówi: „Najważniejsze w matematyce jest ruch myśli, nowe idee”. To właśnie ten twórczy lot myśli generuje twierdzenie Pitagorasa – nie bez powodu ma ono tak wiele różnych dowodów. Pomaga wyjść poza granice tego, co znajome i spojrzeć na znajome rzeczy w nowy sposób.
Wniosek
Ten artykuł został stworzony, abyś mógł spojrzeć poza szkolny program nauczania w matematyce i dowiedzieć się nie tylko dowodów twierdzenia Pitagorasa, które są podane w podręcznikach „Geometria 7-9” (L. S. Atanasyan, V. N. Rudenko) i „Geometria 7” -11 "(AV Pogorelov), ale także inne ciekawe sposoby na udowodnienie słynnego twierdzenia. Zobacz także przykłady zastosowania twierdzenia Pitagorasa w życiu codziennym.
Po pierwsze, te informacje pozwolą Ci zakwalifikować się do wyższych wyników na lekcjach matematyki - informacje na ten temat z dodatkowych źródeł zawsze są wysoko cenione.
Po drugie, chcieliśmy pomóc Ci poczuć, jak interesująca jest matematyka. Upewnij się na konkretnych przykładach, że zawsze jest w nim miejsce na kreatywność. Mamy nadzieję, że twierdzenie Pitagorasa i ten artykuł zainspirują Cię do własnych poszukiwań i ekscytujących odkryć w matematyce i innych naukach.
Powiedz nam w komentarzach, czy uważasz, że dowody w tym artykule są interesujące. Czy te informacje były dla Ciebie przydatne podczas studiów? Napisz do nas, co myślisz o twierdzeniu Pitagorasa i tym artykule - z przyjemnością omówimy to wszystko z Tobą.
blog, z pełnym lub częściowym skopiowaniem materiału, wymagany jest link do źródła.