The potential for creativity is usually attributed to the humanities, leaving the natural sciences with analysis, a practical approach and a dry language of formulas and numbers. Mathematics cannot be attributed to humanitarian subjects. But without creativity in the "queen of all sciences" you will not go far - people have known about this for a long time. Since the time of Pythagoras, for example.
School textbooks, unfortunately, usually do not explain that in mathematics it is important not only to cram theorems, axioms and formulas. It is important to understand and feel its fundamental principles. And at the same time try to free your mind from cliches and elementary truths - only in such conditions all great discoveries are born.
These discoveries include what we know today as the Pythagorean theorem. With its help, we will try to show that mathematics not only can, but should be exciting. And that this adventure is suitable not only for nerds in thick glasses, but for everyone who is strong in mind and strong in spirit.
From the history of the issue
Strictly speaking, although the theorem is called the "Pythagorean theorem", Pythagoras himself did not discover it. The right-angled triangle and its special properties were studied long before it. There are two opposite points of view on this issue. According to one version, Pythagoras was the first to find a complete proof of the theorem. According to another, the proof does not belong to the authorship of Pythagoras.
Today you cannot check who is right and who is wrong. It is only known that the proof of Pythagoras, if it ever existed, has not survived. However, there are suggestions that the famous proof from Euclid's "Elements" may belong to Pythagoras, and Euclid only recorded it.
It is also known today that problems about a right-angled triangle are found in Egyptian sources of the time of Pharaoh Amenemhat I, on Babylonian clay tablets of the period of the reign of King Hammurabi, in the ancient Indian treatise "Sulva sutra" and the ancient Chinese composition "Zhou-bi suan jin".
As you can see, the Pythagorean theorem has occupied the minds of mathematicians since ancient times. There are about 367 different pieces of evidence that exist today as well. In this, no other theorem can compete with it. Famous proof-writers include Leonardo da Vinci and the twentieth President of the United States, James Garfield. All this speaks of the extreme importance of this theorem for mathematics: most of the theorems of geometry are derived from it or in one way or another connected with it.
Proof of the Pythagorean theorem
In school textbooks, mostly algebraic proofs are given. But the essence of the theorem is in geometry, so let's consider first of all those proofs of the famous theorem, which are based on this science.
Proof 1
For the simplest proof of the Pythagorean theorem for a right-angled triangle, you need to set ideal conditions: let the triangle be not only right-angled, but also isosceles. There is reason to believe that this triangle was originally considered by the mathematicians of antiquity.
Statement "A square built on the hypotenuse of a right-angled triangle is equal to the sum of the squares built on its legs" can be illustrated by the following drawing:
Look at an isosceles right-angled triangle ABC: On the hypotenuse AC, you can build a square consisting of four triangles equal to the original ABC. And on the legs AB and BC it is built in a square, each of which contains two similar triangles.
By the way, this drawing formed the basis of numerous anecdotes and cartoons dedicated to the Pythagorean theorem. The most famous is perhaps "Pythagorean pants are equal in all directions":

Proof 2
This method combines algebra and geometry and can be seen as a variant of the ancient Indian proof of the mathematician Bhaskari.
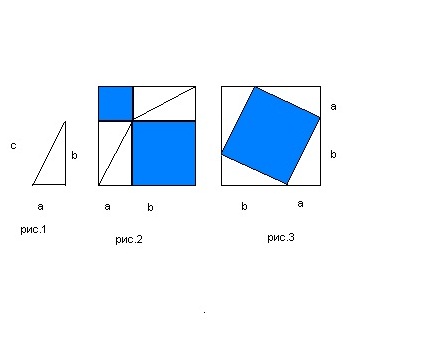
Construct a right-angled triangle with sides a, b and c(fig. 1). Then build two squares with sides equal to the sum of the lengths of the two legs, - (a + b)... In each of the squares, construct as in Figures 2 and 3.
In the first square, build four of the same triangles as in Figure 1. The result is two squares: one with side a, the other with side b.
In the second square, four constructed similar triangles form a square with a side equal to the hypotenuse c.
The sum of the areas of the constructed squares in Fig. 2 is equal to the area of the square we constructed with side c in Fig. 3. This can be easily verified by calculating the areas of the squares in Fig. 2 by the formula. And the area of the inscribed square in Figure 3. by subtracting the areas of four equal inscribed in a square right triangles from the area of a large square with a side (a + b).
Writing all this down, we have: a 2 + b 2 = (a + b) 2 - 2ab... Expand the brackets, carry out all the necessary algebraic calculations and get that a 2 + b 2 = a 2 + b 2... In this case, the area inscribed in Fig. 3. square can be calculated using the traditional formula S = c 2... Those. a 2 + b 2 = c 2- you proved the Pythagorean theorem.
Proof 3
The very same ancient Indian proof is described in the XII century in the treatise "The Crown of Knowledge" ("Siddhanta Shiromani") and as the main argument the author uses the appeal addressed to the mathematical talents and observation of students and followers: "Look!"
But we will analyze this proof in more detail:
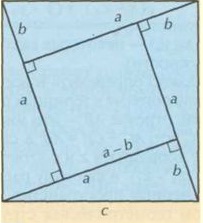
Inside the square, draw four right-angled triangles as indicated in the drawing. The side of the large square, it is also the hypotenuse, we denote with... The legs of the triangle are called a and b... According to the drawing, the side of the inner square is (a-b).
Use the area of a square formula S = c 2 to calculate the area of the outer square. And at the same time, calculate the same value by adding the area of the inner square and the areas of all four right-angled triangles: (a-b) 2 2 + 4 * 1 \ 2 * a * b.
You can use both options for calculating the area of a square to make sure they give the same result. And that gives you the right to write down that c 2 = (a-b) 2 + 4 * 1 \ 2 * a * b... As a result of the solution, you will receive the formula of the Pythagorean theorem c 2 = a 2 + b 2... The theorem is proved.
Proof 4
This curious ancient Chinese proof is called the "Bride's Chair" - because of the chair-like figure that is obtained as a result of all the constructions:
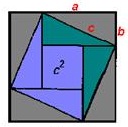

It uses the drawing that we already saw in Figure 3 in the second proof. And the inner square with side c is constructed in the same way as in the ancient Indian proof given above.
If you mentally cut off two green right-angled triangles from the drawing in Fig. 1, move them to the opposite sides of the square with side c and hypotenuses, attach to the hypotenuses of lilac triangles, you get a figure called "bride's chair" (Fig. 2). For clarity, you can do the same with paper squares and triangles. You will see that the "bride's chair" form two squares: small with a side b and big with a side a.
These constructions allowed the ancient Chinese mathematicians and we, following them, to come to the conclusion that c 2 = a 2 + b 2.
Proof 5
This is another way to find a solution to the Pythagorean theorem, relying on geometry. It's called The Garfield Method.
Construct a right triangle ABC... We need to prove that BC 2 = AC 2 + AB 2.
To do this, continue the leg AS and draw a segment CD which is equal to the leg AB... Lower the perpendicular AD section ED... Segments ED and AS are equal. Connect the dots E and V, and E and WITH and get the drawing as in the picture below:
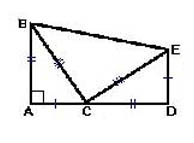
To prove the tower, we again resort to the method we have already tried: find the area of the resulting figure in two ways and equate the expressions to each other.
Find the area of a polygon ABED it is possible by adding the areas of the three triangles that form it. And one of them, ERUs, is not only rectangular, but also isosceles. We also do not forget that AB = CD, AC = ED and BC = CE- this will allow us to simplify the recording and not overload it. So, S ABED = 2 * 1/2 (AB * AC) + 1 / 2BC 2.
Moreover, it is obvious that ABED Is a trapezoid. Therefore, we calculate its area by the formula: S ABED = (DE + AB) * 1 / 2AD... For our calculations, it is more convenient and clear to represent the segment AD as the sum of the segments AS and CD.
Let's write both ways to calculate the area of a figure, putting an equal sign between them: AB * AC + 1 / 2BC 2 = (DE + AB) * 1/2 (AC + CD)... We use the equality of segments already known to us and described above to simplify the right-hand side of the notation: AB * AC + 1 / 2BC 2 = 1/2 (AB + AC) 2... Now let's expand the brackets and transform the equality: AB * AC + 1 / 2BC 2 = 1 / 2AC 2 + 2 * 1/2 (AB * AC) + 1 / 2AB 2... After completing all the transformations, we get exactly what we need: BC 2 = AC 2 + AB 2... We have proved the theorem.
Of course, this list of evidence is far from complete. The Pythagorean theorem can also be proved using vectors, complex numbers, differential equations, stereometry, etc. And even physics: if, for example, liquid is poured into square and triangular volumes similar to those shown in the drawings. By pouring liquid, one can prove the equality of the areas and the theorem itself as a result.
A few words about Pythagorean triplets
This issue is little or not studied in the school curriculum. And yet it is very interesting and of great importance in geometry. Pythagorean triplets are used to solve many mathematical problems. The idea of them can be useful to you in your further education.
So what are Pythagorean triplets? This is the name of the natural numbers, collected in three, the sum of the squares of two of which is equal to the third number squared.
Pythagorean triplets can be:
- primitive (all three numbers are mutually prime);
- not primitive (if each number in the triple is multiplied by the same number, you get a new triplet, which is not primitive).
Even before our era, the ancient Egyptians were fascinated by the mania of the numbers of Pythagorean triplets: in problems they considered a right-angled triangle with sides of 3,4 and 5 units. By the way, any triangle whose sides are equal to the numbers from the Pythagorean triplet is rectangular by default.
Examples of Pythagorean triplets: (3, 4, 5), (6, 8, 10), (5, 12, 13), (9, 12, 15), (8, 15, 17), (12, 16, 20) ), (15, 20, 25), (7, 24, 25), (10, 24, 26), (20, 21, 29), (18, 24, 30), (10, 30, 34), (21, 28, 35), (12, 35, 37), (15, 36, 39), (24, 32, 40), (9, 40, 41), (27, 36, 45), (14 , 48, 50), (30, 40, 50), etc.
Practical application of the theorem
The Pythagorean theorem finds application not only in mathematics, but also in architecture and construction, astronomy and even literature.
First, about construction: the Pythagorean theorem finds wide application in it in problems of various levels of complexity. For example, take a look at a Romanesque window:
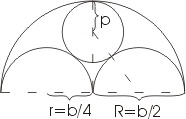
Let's denote the window width as b, then the radius of the semicircle can be denoted as R and express through b: R = b / 2... The radius of the smaller semicircles can also be expressed through b: r = b / 4... In this problem, we are interested in the radius of the inner circle of the window (let's call it p).
The Pythagorean theorem just comes in handy to calculate R... To do this, we use a right-angled triangle, which is indicated by a dotted line in the figure. The hypotenuse of a triangle consists of two radii: b / 4 + p... One leg is a radius b / 4, another b / 2-p... Using the Pythagorean theorem, we write: (b / 4 + p) 2 = (b / 4) 2 + (b / 2-p) 2... Next, we open the brackets and get b 2/16 + bp / 2 + p 2 = b 2/16 + b 2/4-bp + p 2... We transform this expression into bp / 2 = b 2/4-bp... And then we divide all terms by b, we will give similar ones to get 3/2 * p = b / 4... And in the end we will find that p = b / 6- which is what we needed.
Using the theorem, you can calculate the rafter length for a gable roof. Determine how high the mobile tower is needed for the signal to reach a certain settlement. And even permanently set up a Christmas tree in the town square. As you can see, this theorem lives not only on the pages of textbooks, but is often useful in real life.
As for literature, the Pythagorean theorem has inspired writers since antiquity and continues to do so in our time. For example, the nineteenth-century German writer Adelbert von Chamisso was inspired to write a sonnet:
The light of truth will not dissipate soon,
But, shining, it will hardly dissipate
And, like millennia ago,
Will not cause doubt and dispute.
The wisest when it touches the eye
Light of truth, gods are thanked;
And a hundred bulls, stabbed, lie -
A reciprocal gift from the lucky Pythagoras.
Since then, the bulls have been roaring desperately:
Forever alarmed by the bull tribe
The event mentioned here.
It seems to them: the time is about to come
And again they will be sacrificed
Some great theorem.
(translation by Viktor Toporov)
And in the twentieth century, the Soviet writer Yevgeny Veltistov devoted a whole chapter to the proof of the Pythagorean theorem in his book "The Adventures of Electronics". And half a chapter more to the story of the two-dimensional world, which could exist if the Pythagorean theorem became the fundamental law and even religion for a single world. It would be much easier to live in it, but also much more boring: for example, no one there understands the meaning of the words "round" and "fluffy".
And in the book "The Adventures of Electronics" the author, through the mouth of the mathematics teacher Taratar, says: "The main thing in mathematics is the movement of thought, new ideas." It is this creative flight of thought that generates the Pythagorean theorem - it is not for nothing that it has so many different proofs. It helps to go beyond the boundaries of the familiar, and look at familiar things in a new way.
Conclusion
This article was created so that you could look beyond the school curriculum in mathematics and find out not only the proofs of the Pythagorean theorem, which are given in the textbooks "Geometry 7-9" (L. S. Atanasyan, V. N. Rudenko) and "Geometry 7 -11 "(AV Pogorelov), but also other curious ways to prove the famous theorem. And also see examples of how the Pythagorean theorem can be applied in everyday life.
Firstly, this information will allow you to qualify for higher scores in math lessons - information on the subject from additional sources is always highly appreciated.
Secondly, we wanted to help you get a feel for how interesting mathematics is. Make sure with specific examples that there is always a place for creativity in it. We hope that the Pythagorean Theorem and this article will inspire you on your own quest and exciting discoveries in mathematics and other sciences.
Tell us in the comments if you found the evidence in this article interesting. Was this information useful to you in your studies? Write to us what you think about the Pythagorean theorem and this article - we will be pleased to discuss all this with you.
blog. site, with full or partial copying of the material, a link to the source is required.